Filtermaze is a nice cryptography challenge that we solved during Google CTF. The challenge was solved by collaborative efforts with @heromnxpw0 and @l0mb4rdghini (They are goats). Anyway, let’s start with the challenge.
In the handout, we have 3 files
filtermaze.py, our main codegraph.jsonlwe_pub_params.json
Code analysis#
At the beginning of the main, you can see this:
flag = load_flag("flag")
graph_data = load_graph("graph.json")
lwe_params = LWEParams()
<helper for local testing>
with open("lwe_secret_params.json", "r") as s:
lwe_params = json.load(s)
lwe_A = lwe_params.get("A")
lwe_s_key = lwe_params.get("s")
lwe_e_signed = lwe_params.get("e")
lwe_b = lwe_params.get("b")
It is a normal LWE setup here, and it loads the graph.json as graph_data . You can find that we have 2 ways to interact with the server
check_pathget_flag
Here is the check_path block:
if command == "check_path":
segment = client_command.get("segment")
if not isinstance(segment, list):
raise TypeError("Segment must be a list.")
path_result = path_checker.check(segment)
if isinstance(path_result, list):
response_payload = {
"status": "path_complete",
"lwe_error_magnitudes": path_result,
}
elif path_result is True:
response_payload = {"status": "valid_prefix"}
else:
response_payload = {"status": "path_incorrect"}
When we use this command, it will take a list from us and return one of three possible responses. It takes our list and passes it to path_checker.check() . Let’s explore path_checker
class PathChecker:
def __init__(
self,
secret_path,
graph_data,
lwe_error_mags,
):
self.secret_path = secret_path
self.graph = graph_data
self.lwe_error_mags = lwe_error_mags
self.path_len = len(self.secret_path)
def check(self, candidate_segment):
seg_len = len(candidate_segment)
if seg_len > self.path_len:
return False
for i, node in enumerate(candidate_segment):
if node != self.secret_path[i]: # Node mismatch
return False
if i > 0:
prev_node = candidate_segment[i - 1]
neighbors = self.graph.get(prev_node)
if neighbors is None or node not in neighbors:
return False
if seg_len == self.path_len:
error_magnitudes = [int(abs(err_val)) for err_val in self.lwe_error_mags]
return error_magnitudes
else:
return True
So this class needs 3 things to work as expected
- a secret_path
- a graph
- and LWE error mags
the check() will take the provided list from us, and it will start comparing it to the secret path.
- provided path length $>$ length of secret path. It will return
False - Your node $K_i \neq path_i$. It will return
false - If our path didn’t fail in the loop, AND its length is the same as the secret path length, it will return to us error magnitudes
- If we provided the prefix of the secret path, not the full path, it would return true
So when we call this function in main() We will get the LWE error magnitudes if our list is correct. If not, the server will tell us if the prefix is correct or not.
Now with the 2nd functionality of our server, which is get_flag.
elif command == "get_flag":
key_s_raw = client_command.get("lwe_secret_s")
if not isinstance(key_s_raw, list):
raise TypeError("lwe_secret_s must be a list.")
if key_s_raw == lwe_s_key:
response_payload = {"status": "success", "flag": flag}
else:
response_payload = {"status": "invalid_key"}
else:
response_payload = {"status": "error", "message": "Unknown command"}
It is really simple, where it checks if we got the LWE secret s correctly or not. And if we got it right, the server will print the flag. So I think the attack path is clear now, we will try to get the error magnitudes by finding the secret Hamiltonian path, then we will use these errors to break LWE and get s .
Hope you love graph theory <3#
First of all, let’s define what is Hamiltonian path is. A Hamiltonian path is a path that visits each vertex of a graph exactly once. For example,
!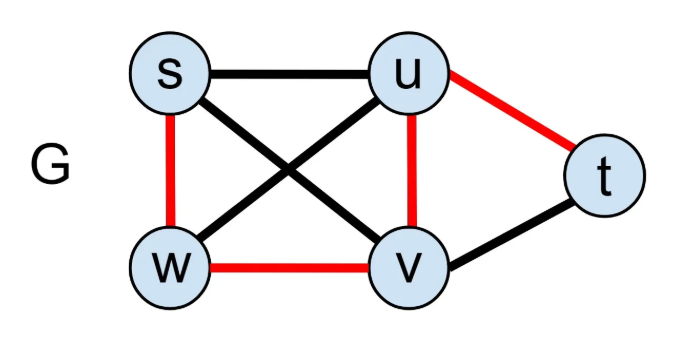
The set of points {T,U,V,W,S} are performing a Hamiltonian path of the graph G . The problem of finding a Hamiltonian path in a graph is an NP-complete problem. And the timing complexity of finding a Hamiltonian path in a graph that consists of N vertices is $O(N!)$. Let’s visualize our graph from the challenge and see
!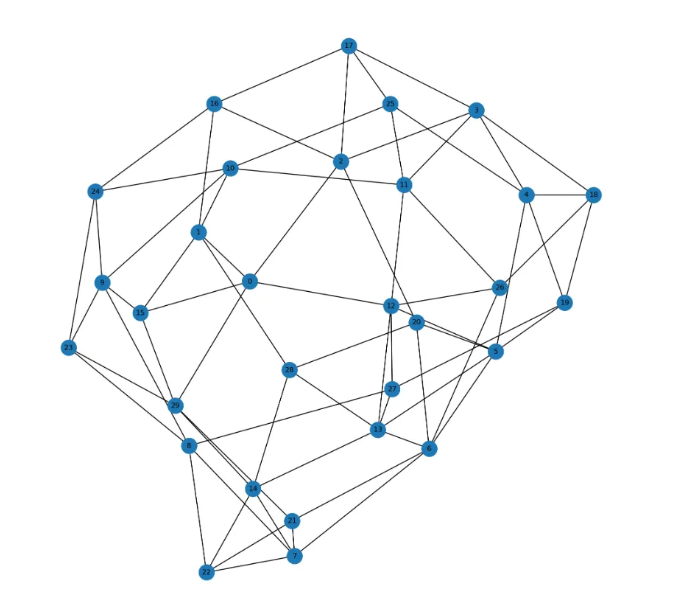
This is the graph from graph.json We need to find a Hamiltonian path in this graph, which is hard. But we can use the server responses to help us, how?. Remember that the server tells you if you have the prefix right or wrong. You don’t need to provide the full path at once. Using this fact, we can brute force to get the path, AND the time complexity is reduced to $O(N^2)$ which is WAYYY better than $O(N!)$. Translating this to code, I was able to get the Hamiltonian path and the LWE error magnitudes.
import socket, subprocess, urllib.request, tempfile, sys, json, re
def recv_until(reader, marker):
for line in reader:
print(line, end='')
if marker in line:
return
raise RuntimeError(f"Connection closed before seeing {marker!r}")
def read_json_response(reader):
while True:
raw = reader.readline()
if raw == "":
raise RuntimeError("Connection closed unexpectedly while waiting for JSON")
if '{' not in raw or '}' not in raw:
continue
start = raw.find('{')
end = raw.rfind('}')
if end < start:
continue
candidate = raw[start:end+1]
try:
return json.loads(candidate)
except json.JSONDecodeError as e:
print(f"[!] JSON parse failed on {candidate!r}: {e}", file=sys.stderr)
continue
def main():
host, port = 'filtermaze.2025.ctfcompetition.com', 1337
print(f"Connecting to {host}:{port} …")
sock = socket.create_connection((host, port))
reader = sock.makefile('r', encoding='utf-8', newline='\\n')
writer = sock.makefile('w', encoding='utf-8', newline='\\n')
recv_until(reader, "Welcome!")
graph = json.load(open("graph.json"))
N = len(graph)
print(f"graph loaded, N = {N}")
path = []
for pos in range(N):
for cand in range(N):
cmd = {"command":"check_path","segment": path + [cand]}
writer.write(json.dumps(cmd) + "\\n")
writer.flush()
resp = read_json_response(reader)
status = resp.get("status")
if status == "valid_prefix":
path.append(cand)
print(f"pos {pos}: found {cand}")
break
elif status == "path_complete":
path.append(cand)
errors = resp.get("lwe_error_magnitudes")
print(f"done!! {path}")
print(f"LWE error magnitudes: {errors}")
return
else:
raise RuntimeError(f"faild at {pos}")
if __name__ == "__main__":
main()
Keep in mind that when you connect to the server, it will ask you to solve PoW, which is outside the scope of the challenge, so I didn’t add the part of the code that solves it. Using this code, I was able to get the path and error magnitudes:
done!! [0, 15, 1, 16, 2, 17, 3, 18, 4, 19, 5, 20, 6, 21, 7, 22, 8, 23, 9, 24, 10, 25, 11, 26, 12, 27, 13, 28, 14, 29]
LWE error magnitudes: [265, 622, 38, 716, 722, 308, 996, 799, 742, 337, 927, 698, 626, 969, 330, 126, 321, 20, 271, 839, 175, 399, 752, 989, 666, 629, 271, 400, 311, 840, 821, 821, 17, 978, 488, 781, 74, 818, 849, 903, 776, 142, 505, 951, 582, 638, 222, 872, 427, 165, 307, 209, 475, 970, 748, 814, 69, 213, 27, 742, 744, 566, 262, 852, 740, 309, 997, 502, 995, 434, 405, 193, 257, 953, 924, 678, 232, 226, 560, 414, 584, 579, 767, 810, 51, 894, 446, 281, 761, 908, 715, 787, 722, 270, 94, 169, 474, 431, 292, 346]
“I hate lattice” time#
Let’s explain first what LWE is. In LWE, there exists a hidden list of $n$ small integers and defined like this
$$s=(s1, s2,\dots,s_n)$$We are given $m$ rows, each a public row of numbers
$$A_{i,*}=(A_{i,1},A_{i,2}, \dots,A_{i,n})$$And also a public parameter $b_i$. Moreover, the following dot product is computed
$$A_{i,*} \cdot{s} = A_{i,1}s_1 + \dots+A_{i,n}s_n$$Then adds a random mistake called the errors $e_i$. Ok, but how $b_i$ is computed?
The thing is that if LWE has no errors, it would be very easy to break using simple linear algebra. But adding the errors to the process adds complexity, and it will not be easy to break and get the secret s . Let’s get back to the challenge so the challenge is giving us the error magnitudes, and this problem should be solved, right? Well, let me say this, but no. The challenge is giving us the error magnitudes, but without the sign of each error. We can think of $e_i$ as $e_i=sign \cdot {mag_i}$ where $sign= \pm 1$.
Re-arrange
Now divide each side by the known magnitude $\mathrm{mag}_i$
$$\frac{A_{i,*}\cdot s - b_i}{\mathrm{mag}_i}= -\,sign\quad\text{(which is either +1 or –1)}.$$the right hand side is exactly the unknown sign that we want. The vector whose last slots are exactly $-\mathrm{sign_1},\dots,-\mathrm{sign_m}$ turns out to be shorter than any random lattice point because those slots are just $\pm 1$ which is not large. Reading the $\pm1$ tells you every sign of the magnitudes and by that we can solve to get s. This is the code we used to get s
import json
from sage.all import *
n = 50
m = 100
q = 1009
def find_signs(A, b, mags):
basis = Matrix(A).augment(Matrix(b).T)
basis_ = []
for i, row in enumerate(basis.rows()):
basis_.append(pow(mags[i], -1, q) * row)
basis = Matrix(basis_).augment(diagonal_matrix([q] * m)).T
lattice = basis.BKZ()
for row in lattice.rows():
if all(x in [-1, 1] for x in row):
return row
def recover_secret(A, b, e, q):
A_mod = Matrix(GF(q), A)
rhs = vector(GF(q), (b - e))
s = A_mod.solve_right(rhs)
return [int(x) % q for x in s]
magnitudes = [265, 622, 38, 716, 722, 308, 996, 799, 742, 337, 927, 698, 626, 969, 330, 126, 321, 20, 271, 839, 175, 399, 752, 989, 666, 629, 271, 400, 311, 840, 821, 821, 17, 978, 488, 781, 74, 818, 849, 903, 776, 142, 505, 951, 582, 638, 222, 872, 427, 165, 307, 209, 475, 970, 748, 814, 69, 213, 27, 742, 744, 566, 262, 852, 740, 309, 997, 502, 995, 434, 405, 193, 257, 953, 924, 678, 232, 226, 560, 414, 584, 579, 767, 810, 51, 894, 446, 281, 761, 908, 715, 787, 722, 270, 94, 169, 474, 431, 292, 346]
data = json.load(open('googleCTF25/crypto-filtermaze/lwe_pub_params.json'))
A = data['A']
b = data['b']
signs = find_signs(A, b, magnitudes)
e = [-signs[i] * magnitudes[i] for i in range(len(signs))]
print(e)
secret = recover_secret(A, vector(b), vector(e), q)
print(secret)
# [476, 307, 600, 197, 240, 777, 484, 151, 334, 229, 183, 106, 695, 176, 410, 795, 49, 886, 690, 743, 5, 790, 918, 466, 239, 300, 159, 786, 550, 572, 95, 77, 145, 742, 82, 71, 332, 597, 992, 1, 71, 17, 192, 133, 513, 795, 508, 218, 329, 403]
#CTF{d4_sup3r_sh0rt_3rr0r_v3ct0r_1s_th3_k3y}
Now we are done with the challenge, all we need is to submit it to the server and the server will give us the flag. AAAAAAAAAAANNND that’s it. See you in the upcoming write-ups (hopefully)
(づ ̄3 ̄)づ╭❤️~